Es gibt eine Vielzahl von Sortieralgorithmen. Das Finden der richtigen Passform für Ihre Anwendung ist eine Aufgabe, die ein kurzes Verständnis der Faktoren wie Leistung, Zeitkomplexität, Codelänge usw. eines bestimmten Algorithmus erfordert. In diesem Beitrag werden wir uns alle wesentlichen Konzepte ansehen, die zur Implementierung von Quicksort in C ++ in der folgenden Reihenfolge erforderlich sind:
- Den Quicksort-Algorithmus verstehen
- Pseudocode für Quicksort
- Programm von Quicksort in C ++
- Zeitkomplexität Quicksort
Den Quicksort-Algorithmus verstehen
So wie Zusammenführen, sortieren , Quicksort folgt der Divide and Conquer-Strategie. Mit der Divide and Conquer-Strategie teilen wir das Problem in viele Teilprobleme auf und lösen sie rekursiv. Zunächst werden wir den gesamten Prozess Schritt für Schritt verstehen und anschließend anhand eines Beispiels ein tiefes Verständnis des gesamten Prozesses entwickeln.
Zuerst werden wir den Benutzer nach dem unsortierten Array fragen.
Sobald wir unser unsortiertes Array haben, müssen wir einen Pivot-Wert aus dem Array auswählen. Wir können jeden Wert wählen.
Sobald wir den Drehpunkt danach ausgewählt haben, müssen wir die anderen Elemente des Arrays so anordnen, dass alle Elemente, die kleiner als der Drehpunkt sind, rechts vom Drehpunkt und alle Elemente größer als der Drehpunkt platziert werden Der Wert ist rechts vom Pivot-Wert zu platzieren.
Wir führen Schritt 3 aus, bis wir unser sortiertes Array erhalten.
Betrachten wir nun ein Beispiel, implementieren den Algorithmus und sehen, wie er funktioniert.
Hallo [5, 4, 1, 11, 9, 6, 2, 3] In diesem Beispiel wird der Pivot immer als das am weitesten rechts stehende Element der Liste betrachtet.
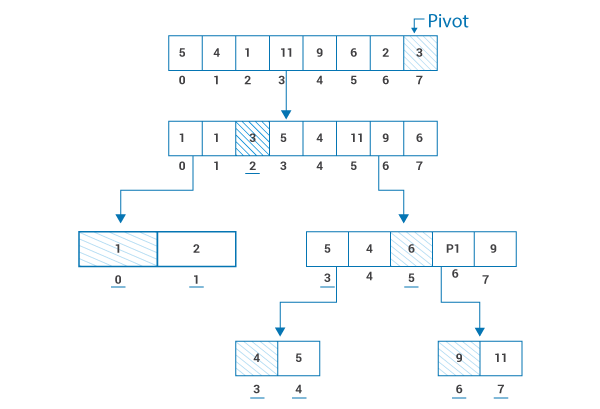
Lassen Sie uns jeden Schritt durchgehen und die Logik verstehen, mit der wir das Problem gelöst haben.
Zuerst haben wir '3' als Drehpunkt ausgewählt und alle Elemente kleiner als '3' rechts und alle Elemente größer als '3' rechts angeordnet.
Zu diesem Zeitpunkt haben wir 2 Teilprobleme. Lösen wir zunächst das Teilproblem rechts. Wir haben einen als Drehpunkt ausgewählt und rechts „2“ platziert.
Um das zweite Teilproblem zu lösen, wählen wir '6' als Drehpunkt und platzieren die Elemente wie oben beschrieben.
Wir haben 2 weitere Unterprobleme. Der erste wird durch Auswahl von 4 als Drehpunkt und der zweite durch Auswahl von 9 als Drehpunkt gelöst. Schließlich haben wir unser sortiertes Array mit den Elementen, die am Unterstreichungsindex platziert sind.
Hinweis- Der wichtige Punkt, den Sie hier verstehen sollten, ist, dass alle Operationen in demselben Array stattfinden. Neue Arrays werden nicht erstellt.
Pseudocode für Quicksort in C ++
QuickSort (Array [], Startindex, Endindex) {if (Startindex Programm von Quicksort in C ++
Wir haben den Algorithmus verstanden und ein tiefes Verständnis für die Funktionsweise des Algorithmus entwickelt. Implementieren wir Quicksort in C ++ und schreiben ein Programm zum Sortieren eines Arrays.
#include using namespace std void swap_elements (int * a, int * b) {int temp = * a * a = * b * b = temp} int partition (int array [], int start_index, int end_index) {int pivot = Array [end_index] int i = (start_index - 1) für (int j = start_index j<= end_index- 1 j++) { if (array[j] <= pivot) { i++ swap_elements(&array[i], &array[j]) } } swap_elements(&array[i + 1], &array[end_index]) return (i + 1) } void quickSort(int array[], int start_index, int end_index) { if (start_index < end_index) { int partition_index = partition(array, start_index, end_index) quickSort(array, start_index, partition_index - 1) quickSort(array, partition_index + 1, end_index) } } void printArray(int array[], int number) { int i cout<<'Sorted Array: ' for (i = 0 i < number i++) cout << array[i] << ' ' cout << endl } int main() { int Hello[30] int i int NumberofElements cout<>Anzahl der Elemente Kosten<<'Enter the elements one by one: ' for(i=0i>Hallo [i]} quickSort (Hallo, 0, NumberofElements-1) printArray (Hallo, NumberofElements) gibt 0 zurück} Ausgabe:
Zeitliche Komplexität
Lassen Sie uns über den wichtigsten Aspekt eines Sortieralgorithmus sprechen, nämlich die zeitliche Komplexität. Es gibt Auskunft über die Leistung des Algorithmus in verschiedenen Szenarien. Diese Werte können uns bei der Entscheidung helfen, ob wir diesen Algorithmus für unsere Anwendung verwenden können.
- I'm besten fall- Auf)
- Durchschnittlicher Fall- (nlogn)
- Schlimmsten Fall- Auf2)
Damit sind wir am Ende dieses Quicksort in C ++ - Artikels angelangt. Wenn Sie mehr erfahren möchten, lesen Sie die von Edureka, einem vertrauenswürdigen Online-Lernunternehmen. Der Java J2EE- und SOA-Schulungs- und Zertifizierungskurs von Edureka wurde entwickelt, um Sie für Kern- und fortgeschrittene Java-Konzepte sowie für verschiedene Java-Frameworks wie Hibernate & Spring zu schulen.
Hast du eine Frage an uns? Bitte erwähne es im Kommentarbereich dieses Blogs und wir werden uns so schnell wie möglich bei dir melden.
Pass by Value vs Pass by Reference Java