Kapselnetzwerke:
Was ist Kapselnetzwerke? Es ist im Grunde ein Netzwerk von verschachtelten neuronalen Schichten.
Ich würde Ihnen empfehlen, auch die folgenden Blogs durchzugehen:
Ich gehe davon aus, dass ihr Convolutional Neural Networks (CNN) kennt. Hier werde ich Ihnen eine kleine Einführung dazu geben, damit ich die Einschränkungen von CNNs diskutieren kann.
Sie können sich auch auf das folgende Video zu Convolutional Neural Network beziehen.
Faltungsneurale Netze (CNN)
Faltungs-Neuronale Netze sind im Grunde genommen Stapel verschiedener Schichten künstlicher Neuronen, die für das Computer-Sehen verwendet werden. Unten habe ich diese Schichten erwähnt:
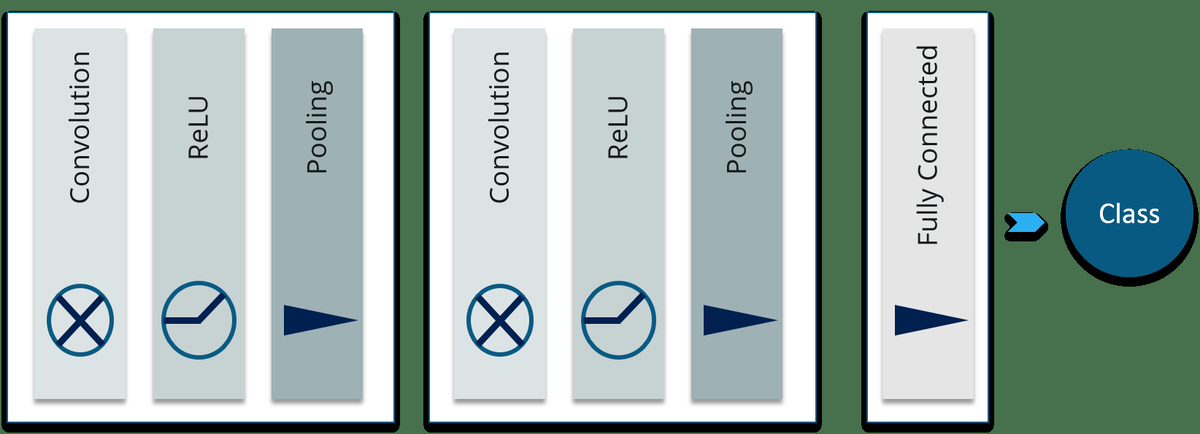
Faltungsschicht: Wenn wir Feedforward-Neuronale Netze (Multi Layer Perceptron) für die Bildklassifizierung verwenden, gibt es viele Herausforderungen. Die frustrierendste Herausforderung besteht darin, dass viele Parameter eingeführt werden. Beachten Sie das Video-Tutorial zu CNN.
Diese Herausforderung bewältigen Faltungsschicht wurde vorgestellt. Es wird angenommen, dass Pixel, die räumlich näher beieinander liegen, bei der Bildung eines bestimmten interessierenden Merkmals viel stärker „zusammenarbeiten“ als Pixel an gegenüberliegenden Ecken des Bildes. Wenn sich herausstellt, dass ein bestimmtes (kleineres) Merkmal beim Definieren der Beschriftung eines Bildes von großer Bedeutung ist, ist es ebenso wichtig, wenn dieses Merkmal unabhängig vom Standort an einer beliebigen Stelle im Bild gefunden wurde.
ReLU-Schicht: Die ReLU-Transformationsfunktion (Rectified Linear Unit) aktiviert einen Knoten nur, wenn der Eingang über einer bestimmten Größe liegt, während der Eingang unter Null liegt. Der Ausgang ist Null. Wenn der Eingang jedoch über einen bestimmten Schwellenwert steigt, besteht eine lineare Beziehung zu abhängige Variable.
- In dieser Ebene entfernen wir alle negativen Werte aus den gefilterten Bildern und ersetzen sie durch Nullen
- Dies geschieht, um zu verhindern, dass die Werte auf Null summiert werden
Pooling Layer: Dies wird verwendet, um ein Downsampling durchzuführen, bei dem kleine und (normalerweise) nicht zusammenhängende Teile des Bildes verbraucht und zu einem einzigen Wert zusammengefasst werden. Es gibt mehrere mögliche Schemata für die Aggregation - das beliebteste Max-Pooling , wobei der maximale Pixelwert in jedem Block genommen wird. Dadurch wird das Netzwerk für kleine Transformationen, Verzerrungen und Übersetzungen im Eingabebild unveränderlich (eine kleine Verzerrung der Eingabe ändert die Ausgabe von Pooling nicht - da wir den Maximal- / Durchschnittswert in einer lokalen Nachbarschaft verwenden).
Vollständig verbundene Ebene: Diese Ebene berechnet die Klassenbewertungen, wobei jede der Zahlen einer Klassenbewertung entspricht. Wie bei gewöhnlichen neuronalen Netzen und wie der Name schon sagt, wird jedes Neuron in dieser Schicht mit allen Neuronen im vorherigen Band verbunden. Kurz gesagt, es führt die endgültige Klassifizierung durch.
Auf diese Weise transformieren ConvNets das Originalbild Schicht für Schicht von den ursprünglichen Pixelwerten in die endgültigen Klassenwerte.
Dies war eine sehr kurze Einführung in Convolutional Neural Networks. Ich würde Ihnen dennoch empfehlen, sich das CNN-Video anzusehen, das ich in diesen Beitrag eingebettet habe.
In diesem Blog von Capsule Networks werde ich nun einige Einschränkungen von Convolutional Neural Networks diskutieren
Einschränkungen von Faltungs-Neuronalen Netzen:
Lassen Sie mich dies mit einer Analogie erklären.
Angenommen, es gibt einen Menschen, dessen Augen die Merkmale verschiedener Bilder erkennen können. Betrachten wir das Gesicht eines Menschen als Beispiel. Dieser unglückliche Kerl kann also verschiedene Merkmale wie Augen, Nase usw. identifizieren, kann jedoch die räumlichen Beziehungen zwischen Merkmalen (Perspektive, Größe, Ausrichtung) nicht identifizieren. Zum Beispiel kann das folgende Bild diesen Kerl täuschen, wenn er es als eine gute Skizze eines menschlichen Gesichts klassifiziert.
Dies ist auch das Problem bei Faltungs-Neuronalen Netzen. CNN kann Merkmale gut erkennen, aktiviert jedoch fälschlicherweise das Neuron für die Gesichtserkennung. Dies liegt daran, dass es weniger effektiv ist, die räumlichen Beziehungen zwischen Merkmalen zu untersuchen.
Ein einfaches CNN-Modell kann die Merkmale für Nase, Augen und Mund korrekt extrahieren, aktiviert jedoch fälschlicherweise das Neuron für die Gesichtserkennung. Ohne die Fehlanpassung in räumlicher Ausrichtung und Größe zu bemerken, ist die Aktivierung für die Gesichtserkennung zu hoch.
Nun, diese Einschränkung ist auf die Max Pooling-Ebene zurückzuführen.
Das maximale Pooling in einem CNN behandelt die Translationsvarianz. Selbst ein Feature wird leicht verschoben. Wenn es sich noch im Pooling-Fenster befindet, kann es dennoch erkannt werden. Trotzdem behält dieser Ansatz nur das maximale Merkmal (das dominierendste) bei und wirft die anderen weg.
Das oben gezeigte Gesichtsbild wird also als normales Gesicht klassifiziert. Die Pooling-Ebene fügt auch diese Art von Invarianz hinzu.
Dies war nie die Absicht der Pooling-Schicht. Das Pooling sollte positionelle, orientierende, proportionale Invarianzen einführen.
In Wirklichkeit fügt diese Pooling-Schicht alle Arten von Positionsinvarianzen hinzu. Wie Sie auch im obigen Diagramm sehen können, führt dies zu dem Dilemma, das Gesicht korrekt zu erkennen.
Mal sehen, welche Lösung von vorgeschlagen wird Geoffrey Hinton .
Wie kann man dieses Problem lösen?
Nun stellen wir uns vor, dass jedes Neuron die Wahrscheinlichkeit sowie die Eigenschaften der Merkmale enthält. Beispielsweise wird ein Vektor ausgegeben, der [Wahrscheinlichkeit, Ausrichtung, Größe] enthält. Mit diesen räumlichen Informationen können wir die Inkonsistenz in der Ausrichtung und Größe der Nasen-, Augen- und Ohrmerkmale erkennen und daher eine viel geringere Aktivierung für die Gesichtserkennung ausgeben.
In dem von Geoffrey Hinton Diese Arten von Neuronen werden Kapseln genannt. Diese Kapseln geben einen Vektor anstelle eines einzelnen Skalierungswerts aus.
Lassen Sie mich die Capsule Networks beleuchten.
Was sind Kapselnetzwerke?
Kapsel ist im Grunde eine Menge verschachtelter neuronaler Schichten. Der Zustand der Neuronen in einer Kapsel erfasst die verschiedenen Eigenschaften wie - Pose (Position, Größe, Orientierung), Verformung, Geschwindigkeit, Textur usw. einer Entität innerhalb eines Bildes.
Anstatt ein Merkmal mit einer bestimmten Variante zu erfassen, wird eine Kapsel trainiert, um die Wahrscheinlichkeit eines Merkmals und seiner Variante zu erfassen. Der Zweck der Kapsel besteht also nicht nur darin, ein Merkmal zu erkennen, sondern auch das Modell zu trainieren, um die Variante zu lernen.
So dass dieselbe Kapsel dieselbe Objektklasse mit unterschiedlichen Ausrichtungen erkennen kann (z. B. im Uhrzeigersinn drehen):
Wir können sagen, dass es auf Äquivarianz und nicht auf Invarianz funktioniert.
Invarianz: ist die Erkennung von Merkmalen unabhängig von den Varianten. Beispielsweise erkennt ein Nasenerkennungsneuron eine Nase unabhängig von der Ausrichtung.
Äquivarianz: ist die Erkennung von Objekten, die sich ineinander verwandeln können (z. B. das Erkennen von Gesichtern mit unterschiedlichen Ausrichtungen). Intuitiv erkennt das Kapselnetzwerk, dass das Gesicht um 31 ° nach rechts gedreht ist (Äquivarianz), anstatt zu realisieren, dass das Gesicht einer Variante entspricht, die um 31 ° gedreht ist. Indem wir das Modell zwingen, die Merkmalsvariante in einer Kapsel zu lernen, können wir mögliche Varianten mit weniger Trainingsdaten effektiver extrapolieren. Darüber hinaus können wir Gegner effektiver ablehnen.
Wie erstelle ich ein dynamisches Array in Java?
Eine Kapsel gibt einen Vektor aus, um die Existenz der Entität darzustellen. Die Ausrichtung des Vektors repräsentiert die Eigenschaften der Entität.
Der Vektor wird an alle möglichen Eltern im neuronalen Netzwerk gesendet. Für jeden möglichen Elternteil kann eine Kapsel einen Vorhersagevektor finden. Der Vorhersagevektor wird basierend auf der Multiplikation des eigenen Gewichts und einer Gewichtsmatrix berechnet. Welcher Elternteil das größte skalare Vorhersagevektorprodukt hat, erhöht die Kapselbindung. Der Rest der Eltern verringert ihre Bindung. Dies wird als bezeichnet Routing nach Vereinbarung .
Dies ist definitiv ein besserer Ansatz als das maximale Pooling, bei dem das Routing auf dem stärksten in der unteren Schicht erkannten Merkmal basiert.
Danach wird eine Squashing-Funktion hinzugefügt. Dies geschieht, um Nichtlinearität einzuführen. Diese Quetschfunktion wird auf die Vektorausgabe jeder Kapsel angewendet.
Lassen Sie mich Ihnen jetzt sagen, wie Capsule Networks funktionieren.
Wie funktionieren Kapselnetzwerke?
Machen wir einen Schritt zurück. In einem vollständig verbundenen Netzwerk ist die Ausgabe jedes Neurons die gewichtete Summe der Eingaben.
Nun wollen wir sehen, was in Capsule Networks passiert.
Neuronales Kapselnetz:
Betrachten wir ein Capsule Neural Network, in dem „uichIst der Aktivitätsvektor für die Kapselich'in der Schicht darunter.
Schritt - 1: Wenden Sie eine Transformationsmatrix anIMijzum Kapselausgang uich der vorherigen Schicht. Zum Beispiel transformieren wir mit einer m × k-Matrix ein k-Duich zu einem m-Du ^j | i. ((m × k) × (k × 1) = m × 1).
Es ist die Vorhersage ( Abstimmung ) von der Kapsel 'i' am Ausgang der Kapsel 'j' oben. „V.jIst der Aktivitätsvektor für die Kapselj ’in der Schicht darüber
Schritt - 2: Berechnen Sie eine gewichtete Summe sjmit Gewichtencij.cijsind die Kopplungskoeffizienten. Die Summe dieser Koeffizienten ist gleich eins. Dies ist der eigentliche Parameter, der sich auf die Beziehung der Kapselgruppe bezieht, über die wir zuvor gesprochen haben.
Schritt - 3: In Convolutional Neural Networks haben wir die ReLU-Funktion verwendet. Hier wenden wir eine Squashing-Funktion an, um den Vektor zwischen 0 und Längeneinheit zu skalieren. Es verkleinert kleine Vektoren auf Null und lange Vektoren auf Einheitsvektoren. Daher ist die Wahrscheinlichkeit jeder Kapsel zwischen null und eins begrenzt.
Es ist die Vorhersage ( Abstimmung ) von der Kapsel 'i' am Ausgang der Kapsel 'j' oben. Wenn der Aktivitätsvektor eine enge Ähnlichkeit mit dem Vorhersagevektor aufweist, schließen wir, dass die Kapselich'ist eng mit der Kapsel verwandtj ’. (Zum Beispiel ist die Nasenkapsel stark mit der Gesichtskapsel verwandt.) Diese Ähnlichkeit wird unter Verwendung des Skalarprodukts des Vorhersage- und Aktivitätsvektors gemessen. Daher berücksichtigt die Ähnlichkeit sowohl die Wahrscheinlichkeit als auch die Merkmalseigenschaften. (statt nur Wahrscheinlichkeit in Neuronen).
Schritt - 4: Berechnen Sie die Relevanzbewertung „bij„. Es ist das Punktprodukt des Aktivitätsvektors und des Vorhersagevektors. Die Kopplungskoeffizientencichjwird als Softmax von berechnetbichj::
Der Kopplungskoeffizient cijwird als Softmax von b berechnetij.
Dieses Bijwird iterativ in mehreren Iterationen aktualisiert.
Dies wird als bezeichnet Routing nach Vereinbarung .
Das folgende Diagramm ist ein Beispiel:
Nach diesem Blog über Capsule Networks werde ich einen Blog über die Implementierung von Capsule Neural Network mit TensorFlow erstellen.
Ich hoffe, Sie haben es genossen, diesen Blog in Kapselnetzwerken zu lesen von Edureka, einem vertrauenswürdigen Online-Lernunternehmen mit einem Netzwerk von mehr als 250.000 zufriedenen Lernenden auf der ganzen Welt. Der Edureka Deep Learning mit TensorFlow-Zertifizierungstraining hilft den Lernenden, Experten für das Training und die Optimierung grundlegender und faltungsbedingter neuronaler Netze zu werden, indem sie Echtzeitprojekte und -aufgaben zusammen mit Konzepten wie SoftMax-Funktion, Auto-Encoder-Neuronalen Netzen und Restricted Boltzmann Machine (RBM) verwenden.
Hast du eine Frage an uns? Bitte erwähnen Sie es in den Kommentaren und wir werden uns bei Ihnen melden.