Deep Learning mit Python: Leitfaden für Anfänger zum Deep Learning

ist eines der heißesten Themen von 2018-19 und das aus gutem Grund. Es gab so viele Fortschritte in der Branche, dass die Zeit gekommen ist, in der Maschinen oder Computerprogramme tatsächlich den Menschen ersetzen. Dies Deep Learning mit Python Der Artikel hilft Ihnen zu verstehen, was genau Deep Learning ist und wie dieser Übergang ermöglicht wurde. In diesem Artikel werde ich die folgenden Themen behandeln:

• Data Science und seine Komponenten
• Das Bedürfnis nach tiefem Lernen
• Was ist Deep Learning?
• Perceptron und künstliche neuronale Netze
• Anwendungen des Deep Learning
• Warum Python für Deep Learning?
• Deep Learning mit Python: Perceptron-Beispiel
• Deep Learning mit Python: Erstellen eines Deep Neural Network

Data Science und seine Komponenten

Nun, Data Science ist etwas, das es schon seit Ewigkeiten gibt. Datenwissenschaft ist die Extraktion von Wissen aus Daten unter Verwendung verschiedener Techniken und Algorithmen.

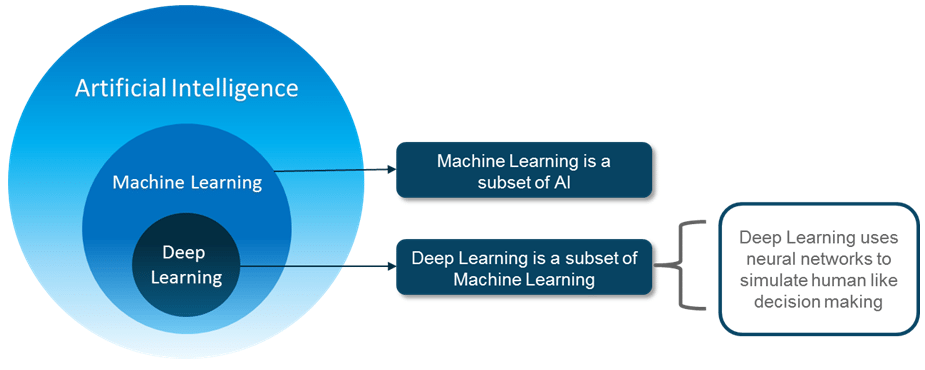
ist eine Technik, die es Maschinen ermöglicht, menschliches Verhalten nachzuahmen. Die Idee hinter AI ist ziemlich einfach und doch faszinierend: Intelligente Maschinen zu entwickeln, die selbst Entscheidungen treffen können. Jahrelang wurde angenommen, dass Computer niemals der Leistung des menschlichen Gehirns entsprechen würden.

Nun, damals hatten wir nicht genug Daten und Rechenleistung, aber jetzt mit Große Daten Mit der Einführung von GPUs ist künstliche Intelligenz möglich.

Was ist der Unterschied zwischen XML und HTML

ist eine Teilmenge der KI-Technik, die statistische Methoden verwendet, damit sich Maschinen mit der Erfahrung verbessern können.

Tiefes Lernen ist eine Teilmenge von ML, die die Berechnung eines mehrschichtigen neuronalen Netzwerks ermöglicht. Es verwendet neuronale Netze, um menschenähnliche Entscheidungen zu simulieren.

Das Bedürfnis nach tiefem Lernen

Ein Schritt in Richtung künstlicher Intelligenz ist maschinelles Lernen. Maschinelles Lernen ist eine Teilmenge der KI und basiert auf der Idee, dass Maschinen Zugriff auf Daten erhalten und für sich selbst lernen und erforschen sollten. Es befasst sich mit der Extraktion von Mustern aus großen Datenmengen. Der Umgang mit großen Datenmengen war kein Problem.

• Algorithmen für maschinelles Lernen kann nicht mit hochdimensionalen Daten umgehen - wo wir eine große Anzahl von Ein- und Ausgängen haben: rund Tausende von Dimensionen. Die Handhabung und Verarbeitung solcher Daten wird sehr komplex und ressourcenintensiv. Dies wird als bezeichnet Fluch der Dimensionalität.

• Eine weitere Herausforderung bestand darin, die zu extrahierende Funktionen . Dies spielt eine wichtige Rolle bei der Vorhersage des Ergebnisses sowie bei der Erzielung einer besseren Genauigkeit. Daher ohne Merkmalsextraktion, Die Herausforderung für den Programmierer nimmt zu, da die Effektivität des Algorithmus sehr stark davon abhängt, wie aufschlussreich der Programmierer ist.

Hier kam Deep Learning zur Rettung. Tiefes Lernen ist fähig, die hochdimensionalen Daten zu verarbeiten und ist auch effizient in Konzentration auf die richtigen Funktionen allein.

Was ist Deep Learning?

Deep Learning ist eine Teilmenge des maschinellen Lernens, bei der ähnliche Algorithmen für maschinelles Lernen zum Trainieren verwendet werden um eine bessere Genauigkeit in den Fällen zu erzielen, in denen der erstere nicht der Marke entsprach. Grundsätzlich, Deep Learning ahmt die Funktionsweise unseres Gehirns nach es lernt aus Erfahrung.

Wie du weißt,Unser Gehirn besteht aus Milliarden von Neuronen das erlaubt uns, erstaunliche Dinge zu tun. Sogar das Gehirn eines kleinen Kindes ist in der Lage, komplexe Probleme zu lösen, die selbst mit Supercomputern sehr schwer zu lösen sind. Wie können wir also die gleiche Funktionalität in einem Programm erreichen? Hier verstehen wir Künstliches Neuron (Perceptron) und Künstliche neuronale Netz.

Perceptron und künstliche neuronale Netze

Deep Learning untersucht die Grundeinheit eines Gehirns, die als Gehirnzelle oder Neuron bezeichnet wird. Lassen Sie uns nun die Funktionalität biologischer Neuronen verstehen und wie wir diese Funktionalität in der Wahrnehmung oder einem künstlichen Neuron nachahmen.

• Dendrit: Empfängt Signale von anderen Neuronen
• Zellkörper: Summiert alle Eingaben
• Axon: Es wird verwendet, um Signale an die anderen Zellen zu übertragen

Ein künstliches Neuron oder ein Perceptron ist ein lineares Modell für die binäre Klassifizierung. Es modelliert ein Neuron mit einer Reihe von Eingaben, von denen jede ein bestimmtes Gewicht erhält. Das Neuron berechnet daraus eine Funktion gewichtet Eingaben und gibt die Ausgabe.

Es empfängt n Eingaben (entsprechend jeder Funktion). Es summiert dann diese Eingaben, wendet eine Transformation an und erzeugt eine Ausgabe. Es hat zwei Funktionen:

• Summe
• Transformation (Aktivierung)

Das Gewicht zeigt die Wirksamkeit einer bestimmten Eingabe. Je höher das Gewicht der Eingabe, desto mehr wirkt sich dies auf das neuronale Netzwerk aus . Andererseits, Vorspannen ist ein zusätzlicher Parameter im Perceptron, mit dem die Ausgabe zusammen mit der gewichteten Summe der Eingaben in das Neuron angepasst wird, wodurch das Modell so unterstützt wird, dass es am besten zu den angegebenen Daten passt.

Aktivierungsfunktionen übersetzt die Eingänge in Ausgänge. Es verwendet einen Schwellenwert, um eine Ausgabe zu erzeugen. Es gibt viele Funktionen, die als Aktivierungsfunktionen verwendet werden, wie z.

• Linear oder Identität
• Einheit oder binärer Schritt
• Sigmoid oder Logistik
• Tanh
• ReLU
• Softmax

Gut. Wenn Sie glauben, dass Perceptron das Problem löst, liegen Sie falsch. Es gab zwei Hauptprobleme:

• Einschichtige Perzeptrone kann nicht linear trennbare Datenpunkte nicht klassifizieren .
• Komplexe Probleme, die damit verbunden sind viele Parameter kann nicht durch einschichtige Perzeptrone gelöst werden.

Betrachten Sie das Beispiel hier und die Komplexität der Parameter, um eine Entscheidung des Marketingteams zu treffen.

Ein Neuron kann nicht so viele Eingaben aufnehmen, und deshalb würde mehr als ein Neuron verwendet, um dieses Problem zu lösen. Neuronales Netz ist wirklich nur ein Zusammensetzung der Perceptrons, auf unterschiedliche Weise verbunden und Betrieb mit verschiedenen Aktivierungsfunktionen.

• Eingabeknoten Bereitstellung von Informationen aus der Außenwelt für das Netzwerk und zusammen als „Eingabeebene“ bezeichnet.
• Versteckte Knoten Führen Sie Berechnungen durch und übertragen Sie Informationen von den Eingabeknoten zu den Ausgabeknoten. Eine Sammlung versteckter Knoten bildet eine „versteckte Ebene“.
• Ausgabeknoten werden gemeinsam als „Ausgabeschicht“ bezeichnet und sind für die Berechnung und Übertragung von Informationen vom Netzwerk nach außen verantwortlich.

Nachdem Sie nun eine Vorstellung davon haben, wie sich ein Perzeptron verhält, welche Parameter beteiligt sind und welche Schichten ein neuronales Netzwerk aufweist, setzen wir dieses Deep Learning mit Python Blog fort und sehen uns einige coole Anwendungen von Deep Learning an.

Anwendungen des Deep Learning

Es gibt verschiedene Anwendungen von Deep Learning in der Branche. Hier sind einige der wichtigsten, die in unseren täglichen Aufgaben enthalten sind.

• Spracherkennung

• Maschinenübersetzung

• Gesichtserkennung und automatische Kennzeichnung

• Virtuelle persönliche Assistenten

• Selbstfahrendes Auto

• Chatbots

Warum Python für Deep Learning?

• ist ein solches Werkzeug, das ein einzigartiges Attribut hat, nämlich a zu sein Allzweck-Programmiersprache als zu sein Einfach zu verwenden wenn es um analytisches und quantitatives Computing geht.
• Es ist sehr einfach zu verstehen
• Python ist Dynamisch getippt
• Enorm
• Eine große Auswahl an Bibliotheken für verschiedene Zwecke wie Numpy, Seaborn, Matplotlib, Pandas und Scikit lernen

Lassen Sie uns anhand eines kleinen, aber aufregenden Beispiels sehen, wie wir Deep Learning mit Python starten können.

Deep Learning mit Python: Perceptron-Beispiel

Jetzt bin ich sicher, dass ihr mit der Arbeitsweise der ' ODER' Tor. Die Ausgabe ist ein wenn einer der Eingänge auch ist ein.

Daher kann ein Perceptron als Trennzeichen oder als Entscheidungslinie verwendet werden, die den Eingabesatz von OR Gate in zwei Klassen unterteilt:

Klasse 1: Eingänge mit einem Ausgang als 0, der unterhalb der Entscheidungslinie liegt.
Klasse 2: Eingänge mit einem Ausgang von 1, der über der Entscheidungslinie oder dem Trennzeichen liegt.

Bisher haben wir verstanden, dass ein lineares Perzeptron verwendet werden kann, um den Eingabedatensatz in zwei Klassen zu klassifizieren. Aber wie klassifiziert es die Daten tatsächlich?

Mathematisch kann ein Perzeptron als eine Gleichung aus Gewichten, Eingaben und Vorspannung betrachtet werden.

Schritt 1: Importieren Sie alle erforderlichen Bibliotheken

Hier werde ich nur eine Bibliothek importieren, dh. TensorFlow

Tensorflow als tf importieren

Schritt 2: Definieren Sie Vektorvariablen für Eingabe und Ausgabe

Als nächstes müssen wir Variablen zum Speichern der Eingabe, Ausgabe und Vorspannung für das Perceptron erstellen.

train_in = [[0,0,1], [0,1,1], [1,0,1], [1,1,1]] train_out = [[0], [1], [1], [1]]

Schritt 3: Gewichtsvariable definieren

Hier definieren wir die Tensorvariable der Form 3 × 1 für unsere Gewichte und weisen ihr zunächst einige Zufallswerte zu.

Was ist anonyme Klasse in Java

w = tf.Variable (tf.random_normal ([3, 1], seed = 15))

Schritt 4: Definieren Sie Platzhalter für Eingabe und Ausgabe

Wir müssen Platzhalter definieren, damit sie externe Eingaben während des Laufs akzeptieren können.

x = tf.placeholder (tf.float32, [None, 3]) y = tf.placeholder (tf.float32, [None, 1])

Schritt 5: Berechnen Sie die Ausgabe- und Aktivierungsfunktion

Wie zuvor erläutert, wird die von einem Perzeptron empfangene Eingabe zuerst mit den jeweiligen Gewichten multipliziert, und dann werden alle diese gewichteten Eingaben summiert. Dieser summierte Wert wird dann der Aktivierung zugeführt, um das Endergebnis zu erhalten.

Ausgabe = tf.nn.relu (tf.matmul (x, w))

Hinweis: In diesem Fall habe ich verwendet relu als meine Aktivierungsfunktion. Sie können jede der Aktivierungsfunktionen nach Ihren Wünschen nutzen.

Schritt 6: Berechnen Sie die Kosten oder den Fehler

Wir müssen den Cost = Mean Squared Error berechnen, der nichts anderes als das Quadrat der Differenz zwischen Perceptron-Output und gewünschter Output ist.

Verlust = tf.reduce_sum (tf.square (Ausgabe - y))

Schritt 7: Fehler minimieren

Das Ziel eines Perzeptrons ist es, den Verlust oder die Kosten oder den Fehler zu minimieren. Hier verwenden wir also den Gradient Descent Optimizer.

optimizer = tf.train.GradientDescentOptimizer (0.01) train = optimizer.minimize (Verlust)

Schritt 8: Initialisieren Sie alle Variablen

Variablen werden nur mit definiert tf.Variable. Wir müssen also die definierten Variablen initialisieren.

init = tf.global_variables_initializer () sess = tf.Session () sess.run (init)

Schritt 9: Perceptron in Iterationen trainieren

Wir müssen unser Perzeptron trainieren, d. H. Werte von Gewichten und Vorspannung in der aufeinanderfolgenden Iteration aktualisieren, um den Fehler oder Verlust zu minimieren. Hier werde ich unser Perzeptron in 100 Epochen trainieren.

für i im Bereich (100): sess.run (Zug, {x: train_in, y: train_out}) cost = sess.run (Verlust, feed_dict = {x: train_in, y: train_out}) print ('Epoch-- ', i,' - Verlust - ', Kosten)

Schritt 10: Ausgabe

……

……

Wie Sie hier sehen können, begann der Verlust bei 2,07 und endete um 0,27

.

Deep Learning mit Python: Erstellen eines Deep Neural Network

Nachdem wir ein Perzeptron erfolgreich erstellt und für ein ODER-Gatter trainiert haben. Lassen Sie uns diesen Artikel fortsetzen und sehen, wie Sie unser eigenes neuronales Netzwerk von Grund auf neu erstellen können, wo wir eine Eingabeebene, versteckte Ebenen und eine Ausgabeebene erstellen.

wie man Kräfte in Java macht

Wir werden den MNIST-Datensatz verwenden. Der MNIST-Datensatz besteht aus 60.000 Schulungen Proben und 10.000 Tests Beispiele handgeschriebener Ziffernbilder. Die Bilder sind von Größe 28 × 28 Pixel und die Ausgabe kann dazwischen liegen 0-9 .

Die Aufgabe hier besteht darin, ein Modell zu trainieren, das die auf dem Bild vorhandene Ziffer genau identifizieren kann

Zunächst verwenden wir den folgenden Import, um die Druckfunktion von Python 3 in Python 2.6+ zu integrieren. __future__ -Anweisungen müssen sich am Anfang der Datei befinden, da sie grundlegende Dinge in Bezug auf die Sprache ändern und der Compiler sie daher von Anfang an kennen muss

aus __future__ import print_function

Es folgt der Code mit Kommentaren bei jedem Schritt

# MNIST-Daten aus tensorflow.examples.tutorials.mnist importieren import_data importieren mnist = input_data.read_data_sets ('/ tmp / data /', one_hot = True) Tensorflow als tf importieren matplotlib.pyplot als plt # Parameter learning_rate = 0.001 training_epochs = 15 batch_size = 100 display_step = 1 # Netzwerkparameter n_hidden_1 = 256 # Anzahl der Features der 1. Schicht n_hidden_2 = 256 # Anzahl der Features der 2. Schicht n_input = 784 # MNIST-Dateneingabe (Bildform: 28 * 28) n_classes = 10 # MNIST-Gesamtklassen ( 0-9 Stellen) # tf Diagrammeingabe x = tf.placeholder ('float', [None, n_input]) y = tf.placeholder ('float', [None, n_classes]) # Modell def multilayer_perceptron (x, weight) erstellen , Verzerrungen): # Versteckte Ebene mit RELU-Aktivierungsschicht_1 = tf.add (tf.matmul (x, Gewichte ['h1']), Verzerrungen ['b1']) Ebene_1 = tf.nn.relu (Schicht_1) # Versteckte Ebene mit RELU-Aktivierungsschicht_2 = tf.add (tf.matmul (Schicht_1, Gewichte ['h2']), Vorspannung ['b2']) Schicht_2 = tf.nn.relu (Schicht_2) # Ausgangsschicht mit linearer Aktivierung out_layer = tf. Matmul (Schicht _2, Gewichte ['out']) + Verzerrungen ['out'] return out_layer # Speichern von Ebenen weight & Bias weight = {'h1': tf.Variable (tf.random_normal ([n_input, n_hidden_1])), 'h2' : tf.Variable (tf.random_normal ([n_hidden_1, n_hidden_2])), 'out': tf.Variable (tf.random_normal ([n_hidden_2, n_classes]))} biases = {'b1': tf.Variable (tf. random_normal ([n_hidden_1])), 'b2': tf.Variable (tf.random_normal ([n_hidden_2])), 'out': tf.Variable (tf.random_normal ([n_classes]))} # Konstruiere das Modell pred = multilayer_perceptron (x, Gewichte, Verzerrungen) # Definieren Sie Verlust- und Optimierungskosten = tf.reduce_mean (tf.nn.softmax_cross_entropy_with_logits (logits = pred, labels = y)) Optimierer = tf.train.AdamOptimizer (learning_rate = learning_rate) .minimize (cost) # Initialisieren der Variablen init = tf.global_variables_initializer () #Erstellen einer leeren Liste zum Speichern des Kostenverlaufs und des Genauigkeitsverlaufs cost_history = [] Genauigkeitshistorie = [] # Starten Sie das Diagramm mit tf.Session () als sess: sess.run (init ) # Trainingszyklus für Epoche in Reichweite (training_epochs): avg_cost = 0. total_batch = int (mnist.train.num_examples / batch_size) # Schleife über alle Batches für i im Bereich (total_batch): batch_x, batch_y = mnist.train.next_batch (batch_size) # Optimierungsoperation (backprop) und Kosten ausführen op (um den Verlustwert zu erhalten) _, c = sess.run ([Optimierer, Kosten], feed_dict = {x: batch_x, y: batch_y}) # Berechne den durchschnittlichen Verlust avg_cost + = c / total_batch # Zeige Protokolle pro Epochenschritt an, wenn Epoche% display_step == 0: korrekte_Vorhersage = tf.equal (tf.argmax (pred, 1), tf.argmax (y, 1)) # Genauigkeitsgenauigkeit berechnen = tf.reduce_mean (tf.cast (korrekte_Vorhersage, 'float') ) acu_temp = Genauigkeit.eval ({x: mnist.test.images, y: mnist.test.labels}) #Anhängen der Genauigkeit an die Liste Genauigkeit_Geschichte.Anhängen (acu_temp) #Anhängen der Kostenhistorie cost_history.append (avg_cost) print ('Epoche:', '% 04d'% (Epoche + 1), '- Kosten =', '{: .9f}'. Format (avg_cost), '- Genauigkeit =', acu_temp) Druck ('Optimierung abgeschlossen! ') #plotten Sie den Kostenverlauf plt.plot (cost_history) plt.show () #plotten Sie den Genauigkeitsverlauf plt.plot (Genauigkeit _history) plt.show () # Testmodell korrekte_Vorhersage = tf.equal (tf.argmax (pred, 1), tf.argmax (y, 1)) # Berechnen Sie die Genauigkeit Genauigkeit = tf.reduce_mean (tf.cast (korrekte_Vorhersage, ' float ')) print (' Genauigkeit: ', Genauigkeit.eval ({x: mnist.test.images, y: mnist.test.labels}))

Ausgabe:

Damit sind wir am Ende dieses Artikels über Deep Learning with Python angelangt. Ich hoffe, Sie haben ein Verständnis für die verschiedenen Komponenten von Deep Learning, wie alles begann und wie wir mit Python ein einfaches Perzeptron und ein Deep Neural Network erstellen können.

Edurekas wird von Branchenfachleuten gemäß den Anforderungen und Anforderungen der Branche kuratiert. Sie beherrschen die Konzepte wie SoftMax-Funktion, Autoencoder Neural Networks, Restricted Boltzmann Machine (RBM) und arbeiten mit Bibliotheken wie Keras & TFLearn. Der Kurs wurde speziell von Branchenexperten mit Echtzeit-Fallstudien kuratiert.

Hast du eine Frage an uns? Bitte erwähnen Sie es im Kommentarbereich von „Deep Learning with Python“ und wir werden uns bei Ihnen melden.