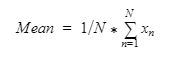Daten zu verstehen und daraus Wert zu schaffen, ist die Fähigkeit des Jahrzehnts. Maschinelles Lernen ist eine solche Kernkompetenz, die Unternehmen dabei hilft, diese zu erfüllen. Um jedoch loszulegen, müssen Sie Ihre Grundlagen richtig aufbauen. In diesem Artikel werde ich einige grundlegende Konzepte behandeln und Ihnen Richtlinien für den Beginn Ihrer Reise in das maschinelle Lernen geben. In diesem Artikel über Statistiken zum maschinellen Lernen werden die folgenden Themen behandelt:
Wahrscheinlichkeit und Statistik für maschinelles Lernen:
Was ist Wahrscheinlichkeit?
Die Wahrscheinlichkeit quantifiziert die Wahrscheinlichkeit des Eintretens eines Ereignisses. Wenn Sie beispielsweise einen fairen, unvoreingenommenen Würfel werfen, ist die Wahrscheinlichkeit von ein Auftauchen ist 1/6 . Nun, wenn Sie sich w fragenhy? Dann ist die Antwort ganz einfach!
Dies liegt daran, dass es sechs Möglichkeiten gibt und alle gleich wahrscheinlich sind (fairer Würfel). Deshalb können wir hinzufügen 1 + 1 + 1 + 1 + 1 + 1 = 6. Aber da interessieren wir uns für die Ereignis, bei dem 1 auftaucht . Es gibt Das Ereignis kann nur auf eine Weise auftreten. Deshalb,
Wahrscheinlichkeit, dass 1 auftaucht = 1/6
Ähnliches gilt für alle anderen Zahlen, da alle Ereignisse gleich wahrscheinlich sind. Einfach, richtig?
Nun, eine häufigere Definition der Wahrscheinlichkeit für dieses Beispiel würde sich so anhören: Die Wahrscheinlichkeit, dass 1 auftaucht, ist das Verhältnis der Häufigkeit, mit der 1 aufgetaucht ist, zur Gesamtzahl der Würfel, wenn der Würfel unendlich oft gewürfelt wurde mal.Wie macht das Sinn?
Machen wir es interessanter. Betrachten Sie die beiden Fälle - Sie haben fünf Mal einen fairen Würfel gewürfelt. In einem Fall ist die Reihenfolge der auftauchenden Zahlen - [1,4,2,6,4,3]. Im anderen Fall erhalten wir - [2,2,2,2,2,2]. Welches ist Ihrer Meinung nach wahrscheinlicher?
Beides ist gleich wahrscheinlich. Scheint seltsam, oder?
Betrachten Sie nun einen anderen Fall, in dem sich jeweils alle 5 Rollen befinden unabhängig . Das heißt, ein Wurf wirkt sich nicht auf den anderen aus. Im ersten Fall, als 6 auftauchte, hatte es keine Ahnung, dass 2 davor auftauchten. Daher sind alle 5 Rollen gleich wahrscheinlich.
In ähnlicher Weise können die geraden 2s im zweiten Fall als eine Folge unabhängiger Ereignisse verstanden werden. Und all diese Ereignisse sind gleich wahrscheinlich. Insgesamt, da wir die gleichen Würfel haben, Die Wahrscheinlichkeit, dass eine bestimmte Zahl in Fall eins auftaucht, ist dieselbe wie in Fall zwei. Lassen Sie uns als nächstes in diesem Artikel über Statistiken für maschinelles Lernen den Begriff verstehen Unabhängigkeit.
Unabhängigkeit
Zwei Ereignisse A und B gelten als unabhängig, wenn das Auftreten von A das Ereignis B nicht beeinflusst . Wenn Sie beispielsweise eine Münze werfen und einen Würfel werfen, hat das Ergebnis des Würfels keinen Einfluss darauf, ob die Münze Kopf oder Zahl zeigt. Auch für zwei unabhängige Ereignisse A und B. , das Wahrscheinlichkeit, dass A und B zusammen auftreten können . Wenn Sie zum Beispiel die Wahrscheinlichkeit haben möchten, dass die Münze Köpfe zeigt und der Würfel 3 zeigt.
Was ist Init in Python
P (A und B) = P (A) · P (B)
Daher ist P = & frac12 (Wahrscheinlichkeit, dass Köpfe auftauchen) * ⅙ (Wahrscheinlichkeit, dass 3 auftauchen) = 1/12
Im vorherigen Beispiel ist für beide Fälle P = ⅙ * ⅙ * ⅙ * ⅙ * ⅙ * ⅙.
Lassen Sie uns nun über Ereignisse sprechen, die nicht unabhängig sind. Betrachten Sie die folgende Tabelle:
| Fettleibig | Nicht fettleibig | |
| Herzprobleme | Vier fünf | fünfzehn |
| Keine Herzprobleme | 10 | 30 |
Eine Umfrage unter 100 Personen wurde durchgeführt. 60 hatten Herzprobleme und 40 nicht. Von den 60 mit Herzproblemen waren 45 fettleibig. Von den 40, die kein Herzproblem hatten, waren 10 fettleibig. Wenn dich jemand fragt -
- Wie hoch ist die Wahrscheinlichkeit eines Herzproblems?
- Wie hoch ist die Wahrscheinlichkeit, ein Herzproblem zu haben und nicht fettleibig zu sein?
Die Antwort auf die ersten Fragen ist einfach - 60/100. Für den zweiten wäre es 15/100. Betrachten Sie nun die dritte Frage: Eine Person wurde zufällig ausgewählt. Es wurde festgestellt, dass er eine Herzkrankheit hatte. Wie groß ist die Wahrscheinlichkeit, dass er fettleibig ist?
Denken Sie jetzt an die Informationen, die Sie erhalten haben. Es ist bekannt, dass er an einer Herzerkrankung leidet. Daher kann er nicht von den 40 sein, die keine Herzkrankheit haben. Es gibt nur 60 mögliche Optionen (die oberste Zeile in der Tabelle). Unter diesen reduzierten Möglichkeiten beträgt die Wahrscheinlichkeit, dass er fettleibig ist, 45/60. Nachdem Sie nun wissen, was unabhängige Ereignisse sind, lassen Sie uns als Nächstes in diesem Artikel über Statistiken für maschinelles Lernen die bedingten Wahrscheinlichkeiten verstehen.
Bedingte Wahrscheinlichkeiten
Um die bedingten Wahrscheinlichkeiten zu verstehen, setzen wir unsere Diskussion mit dem obigen Beispiel fort. Der Status der Fettleibigkeit und der Status des Leidens an Herzproblemen sind nicht unabhängig. Wenn Fettleibigkeit keine Auswirkungen auf Herzprobleme hätte, wäre die Anzahl der Fälle von Fettleibigkeit und Nicht-Fettleibigkeit bei Menschen mit Herzproblemen gleich gewesen.
Außerdem wurde uns mitgeteilt, dass die Person Herzprobleme hat und wir mussten die Wahrscheinlichkeit herausfinden, dass sie fettleibig ist. Die Wahrscheinlichkeit in diesem Fall hängt also davon ab, dass er ein Herzproblem hat. Wenn die Wahrscheinlichkeit des Auftretens von Ereignis A von Ereignis B abhängig ist, stellen wir es als dar
P (A | B)
Nun gibt es einen Satz, der uns hilft, diese bedingte Wahrscheinlichkeit zu berechnen. Es heißt das Bayes-Regel .
P (A | B) = P (A und B) / P (B)
Sie können diesen Satz überprüfen, indem Sie das gerade diskutierte Beispiel einfügen. Wenn Sie dies bisher verstanden haben, können Sie mit den folgenden Schritten beginnen - - Naive Bayes . Es verwendet bedingte Wahrscheinlichkeiten, um zu klassifizieren, ob eine E-Mail ein Spam ist oder nicht. Es kann viele andere Klassifizierungsaufgaben ausführen. Aber im Wesentlichen steht die bedingte Wahrscheinlichkeit im Mittelpunkt von .
Statistiken:
Statistiken sind wird verwendet, um eine große Anzahl von Datenpunkten zusammenzufassen und Rückschlüsse zu ziehen. In Data Science und Machine Learning stoßen Sie häufig auf die folgende Terminologie
- Zentralitätsmaßnahmen
- Verteilungen (besonders normal)
Zentralitätsmaße und Spreadmaße
Bedeuten:
Mittelwert ist nur ein Durchschnitt der Zahlen . Um den Mittelwert herauszufinden, müssen Sie die Zahlen summieren und durch die Anzahl der Zahlen teilen. Zum Beispiel ist der Mittelwert von [1,2,3,4,5] 15/5 = 3.
Median:
Median ist der mittleres Element einer Reihe von Zahlen wenn sie in aufsteigender Reihenfolge angeordnet sind. Zum Beispiel sind die Zahlen [1,2,4,3,5] in aufsteigender Reihenfolge angeordnet [1,2,3,4,5]. Die mittlere davon ist 3. Daher ist der Median 3. Aber was ist, wenn die Anzahl der Zahlen gerade ist und daher keine mittlere Zahl hat? In diesem Fall nehmen Sie den Durchschnitt der beiden mittleren Zahlen. Für eine Folge von 2n Zahlen in aufsteigender Reihenfolge wird der n-te und (n + 1) gemittelt.thZahl, um den Median zu erhalten. Beispiel - [1,2,3,4,5,6] hat den Median (3 + 4) / 2 = 3,5
Modus:
Modus ist einfach der häufigste Zahl in einer Reihe von Zahlen . Zum Beispiel ist der Modus von [1,2,3,3,4,5,5,5] 5.
Varianz:
Varianz ist kein Zentralitätsmaß. Es misst wie Ihre Daten um den Mittelwert verteilt sind . Es wird quantifiziert als
xist der Mittelwert von N Zahlen. Sie nehmen einen Punkt, subtrahieren den Mittelwert, nehmen das Quadrat dieser Differenz. Tun Sie dies für alle N Zahlen und mitteln Sie sie. Die Quadratwurzel der Varianz wird als Standardabweichung bezeichnet. Lassen Sie uns in diesem Artikel über Statistiken zum maschinellen Lernen die Normalverteilung verstehen.
Unterschied zwischen Doktorand und Master
Normalverteilung
Vertrieb hilft uns verstehen, wie unsere Daten verbreitet werden . Zum Beispiel haben wir in einer Stichprobe von Altersgruppen möglicherweise mehr junge Menschen als ältere Erwachsene und daher kleinere Alterswerte mehr als größere Werte. Aber wie definieren wir eine Verteilung? Betrachten Sie das folgende Beispiel
Die y-Achse repräsentiert die Dichte. Der Modus dieser Verteilung ist 30, da es sich um den Peak handelt und daher am häufigsten ist. Wir können auch den Median lokalisieren. Der Median liegt an dem Punkt auf der x-Achse, an dem die Hälfte der Fläche unter der Kurve bedeckt ist. Die Fläche unter jeder Normalverteilung ist 1, da die Summe der Wahrscheinlichkeiten aller Ereignisse 1 ist.
Der Median im obigen Fall liegt bei 4. Dies bedeutet, dass die Fläche unter der Kurve vor 4 dieselbe ist wie die nach 4. Betrachten Sie ein anderes Beispiel
Wir sehen drei Normalverteilungen. Die blauen und roten haben den gleichen Mittelwert. Der rote hat eine größere Varianz. Daher ist es weiter verbreitet als das blaue. Da die Fläche jedoch 1 sein muss, ist die Spitze der roten Kurve kürzer als die blaue Kurve, um die Fläche konstant zu halten.
Ich hoffe, Sie haben die grundlegenden Statistiken und Normalverteilungen verstanden. Lassen Sie uns nun in diesem Artikel über Statistiken zum maschinellen Lernen etwas über die lineare Algebra lernen.
Lineare Algebra
Moderne KI wäre ohne lineare Algebra nicht möglich. Es bildet den Kern von Tiefes Lernen und wurde sogar in einfachen Algorithmen wie verwendet . Beginnen wir ohne weitere Verzögerung.
Sie müssen mit Vektoren vertraut sein. Sie sind eine Art geometrische Darstellungen im Raum. Beispielsweise hat ein Vektor [3,4] 3 Einheiten entlang der x-Achse und 4 Einheiten entlang der y-Achse. Betrachten Sie das folgende Bild -
Der Vektor d1 hat 0,707 Einheiten entlang der x-Achse und 0,707 Einheiten entlang der y-Achse. Ein Vektor hat eine Dimension. Es hat notwendigerweise eine Größe und eine Richtung. Beispielsweise,
Das obige Bild hat einen Vektor (4,3). Seine Größe ist 5 und es macht 36,9 Grad mit der x-Achse.
Was ist nun eine Matrix? Matrix ist ein mehrdimensionales Array von Zahlen. Wofür wird es verwendet? Wir werden voraussehen. Schauen wir uns zunächst an, wie es verwendet wird.
Matrix
Eine Matrix kann viele Dimensionen haben. Betrachten wir eine zweidimensionale Matrix. Es hat Zeilen (m) und Spalten (n). Daher hat es m * n Elemente.
Beispielsweise,
Diese Matrix hat 5 Zeilen und 5 Spalten. Nennen wir es A. Daher ist A (2,3) der Eintrag in der zweiten Zeile und dritten Spalte, der 8 ist.
Nachdem Sie nun wissen, was eine Matrix ist, wollen wir uns die verschiedenen Operationen der Matrix ansehen.
Matrixoperationen
Zugabe von Matrizen
Zwei Matrizen der gleich Dimensionen können hinzugefügt werden. Die Addition erfolgt elementweise.
Skalarmultiplikation
Eine Matrix kann mit einer skalaren Größe multipliziert werden. Eine solche Multiplikation führt dazu, dass jeder Eintrag in der Matrix mit dem Skalar multipliziert wird. Ein Skalar ist nur eine Zahl
Matrix Transponieren
Matrixtransponierung ist einfach. Für eine Matrix A (m, n) sei A 'ihre Transponierte. Dann
A '(i, j) = A (j, i)
Beispielsweise,
Matrix-Multiplikation
Dies ist wahrscheinlich etwas kniffliger als andere Operationen. Bevor wir darauf eingehen, definieren wir das Punktprodukt zwischen zwei Vektoren.
Betrachten Sie den Vektor X = [1,4,6,0] und den Vektor Y = [2,3,4,5]. Dann ist das Punktprodukt zwischen X und Y definiert als
X.Y = 1 * 2 + 4 * 3 + 6 * 4 + 0 * 5 = 38
Es ist also eine elementweise Multiplikation und Addition. Jetzt,Betrachten wir zwei Matrizen A (m, n) und B (n, k), wobei m, n, k Dimensionen und damit ganze Zahlen sind. Wir definieren Matrixmultiplikation als
Im obigen Beispiel wird das erste Element des Produkts (44) durch das Punktprodukt der ersten Reihe der linken Matrix mit der ersten Spalte der rechten Matrix erhalten. In ähnlicher Weise wird 72 durch das Punktprodukt der ersten Reihe der linken Matrix mit der zweiten Spalte der rechten Matrix erhalten.
wie man ein Array PHP druckt
Beachten Sie, dass für die linke Matrix die Anzahl der Spalten der Anzahl der Zeilen in der rechten Spalte entsprechen sollte. In unserem Fall existiert das Produkt AB, aber nicht BA, da m nicht gleich k ist. Für zwei Matrizen A (m, n) und B (n, k) ist das Produkt AB definiert und die Dimension des Produkts ist (m, k) (die äußersten Dimensionen von (m, n), (n, k) )). BA ist jedoch nur definiert, wenn m = k ist.
Damit beenden wir diesen Artikel über Statistiken für maschinelles Lernen. Ich hoffe, Sie haben einige der Jargons des maschinellen Lernens verstanden. Es endet hier jedoch nicht. Um sicherzustellen, dass Sie für die Branche gerüstet sind, können Sie die Edureka-Kurse zu Data Science und KI lesen. Sie können gefunden werden