Die lineare Diskriminanzanalyse ist eine sehr beliebte Technik des maschinellen Lernens, mit der Klassifizierungsprobleme gelöst werden. In diesem Artikel werden wir versuchen, die Intuition und Mathematik hinter dieser Technik zu verstehen. Ein Beispiel für die Implementierung von LDA in R. ist ebenfalls vorhanden.
- Annahme einer linearen Diskriminanzanalyse
- Intuitionen
- Mathematische Beschreibung von LDA
- Modellparameter lernen
- Beispiel in R.
Dann fangen wir an
Annahme einer linearen Diskriminanzanalyse
Die lineare Diskriminanzanalyse basiert auf den folgenden Annahmen:
Die abhängige Variable Y. ist diskret. In diesem Artikel wird davon ausgegangen, dass die abhängige Variable binär ist und Klassenwerte annimmt {+1, -1} . Die Wahrscheinlichkeit, dass eine Stichprobe zur Klasse gehört +1 d.h. P (Y = +1) = p . Daher die Wahrscheinlichkeit, dass eine Stichprobe zur Klasse gehört -ein ist 1-p .
Die unabhängige (n) Variable (n) X. kommen aus Gaußschen Verteilungen. Der Mittelwert der Gaußschen Verteilung hängt von der Klassenbezeichnung ab Y. . wenn Y. ich = +1 , dann der Mittelwert von X. ich ist & # 120583 +1 , sonst ist es & # 120583 -ein . Die Varianz & # 120590 2 ist für beide Klassen gleich. Mathematisch gesehen, X | (Y = +1) ~ N (& # 120583 +1 , & # 120590 2 ) und X | (Y = -1) ~ N (& # 120583 -ein , & # 120590 2 ) , wo N. bezeichnet die Normalverteilung.
Mit diesen Informationen ist es möglich, eine gemeinsame Verteilung aufzubauen P (X, Y) für die unabhängige und abhängige Variable. Daher gehört LDA zur Klasse von Generative Klassifikatormodelle . Ein eng verwandter generativer Klassifikator ist die Quadratic Discriminant Analysis (QDA). Es basiert auf denselben Annahmen der LDA, außer dass die Klassenabweichungen unterschiedlich sind.
Fahren wir mit dem Artikel zur linearen Diskriminanzanalyse fort und sehen wir uns das an
Intuition
Betrachten Sie die klassenbedingten Gaußschen Verteilungen für X. angesichts der Klasse Y. . Die folgende Abbildung zeigt die Dichtefunktionen der Verteilungen. In dieser Abbildung, wenn Y = +1 , dann der Mittelwert von X. ist 10 und wenn Y = -1 Der Mittelwert ist 2. Die Varianz beträgt in beiden Fällen 2.
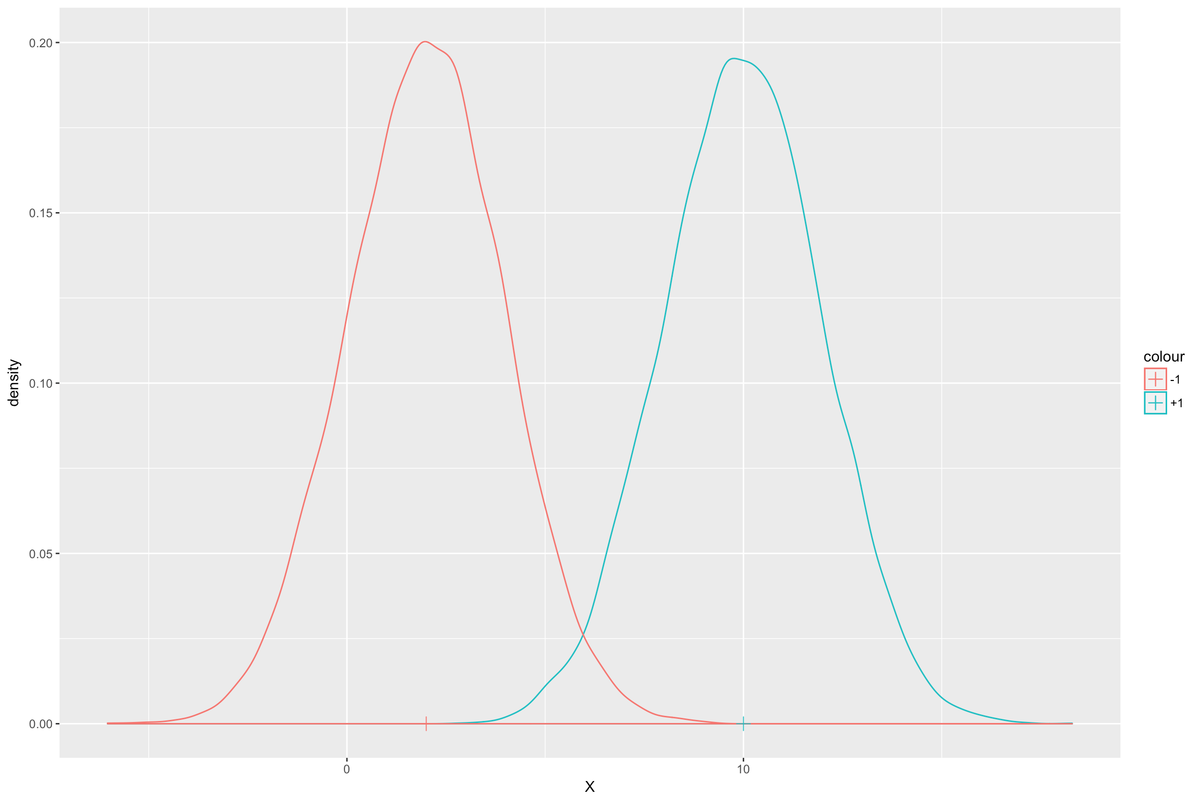
Nehmen wir nun einen neuen Wert von an X. wird uns gegeben. Bezeichnen wir es einfach als x ich . Die Aufgabe besteht darin, die wahrscheinlichste Klassenbezeichnung dafür zu bestimmen x ich d.h. Y. ich . Der Einfachheit halber sei angenommen, dass die Wahrscheinlichkeit p der zur Klasse gehörenden Stichprobe +1 ist das gleiche wie das der Zugehörigkeit zur Klasse -ein d.h. p = 0,5 .
Intuitiv ist es sinnvoll zu sagen, dass wenn x ich ist näher an & # 120583 +1 als es ist zu & # 120583 -ein , dann ist es wahrscheinlicher, dass Y. ich = +1 . Formeller, Y. ich = +1 wenn:
wie man ein Java-Programm beendet
| x ich - & # 120583 +1 |<|x ich - & # 120583 -ein |
Normalisierung beider Seiten durch die Standardabweichung:
| x ich - & # 120583 +1 | / & # 120590<|x ich - & # 120583 -ein | / & # 120590
Quadrieren beider Seiten:
(x ich - & # 120583 +1 ) 2 / & # 120590 2 <(x ich - & # 120583 -ein ) 2 / & # 120590 2
x ich 2 / & # 120590 2 + & # 120583 +1 2 / & # 120590 2 - 2 x ich & # 120583 +1 / & # 120590 2
2 x ich (& # 120583 -ein - & # 120583 +1 ) / & # 120590 2 - (& # 120583 -ein 2 / & # 120590 2 - & # 120583 +1 2 / & # 120590 2 )<0
-2 x ich (& # 120583 -ein - & # 120583 +1 ) / & # 120590 2 + (& # 120583 -ein 2 / & # 120590 2 - & # 120583 +1 2 / & # 120590 2 )> 0
Der obige Ausdruck hat die Form bx ich + c> 0 wo b = -2 (& # 120583 -ein - & # 120583 +1 ) / & # 120590 2 und c = (& # 120583 -ein 2 / & # 120590 2 - & # 120583 +1 2 / & # 120590 2 ) .
sortiere Array Array c ++
Es ist offensichtlich, dass die Form der Gleichung ist linear daher der Name Lineare Diskriminanzanalyse.
Fahren wir mit dem Artikel zur linearen Diskriminanzanalyse fort und sehen,
Mathematische Beschreibung von LDA
Die mathematische Ableitung des Ausdrucks für LDA basiert auf Konzepten wie Bayes-Regel und Bayes Optimal Classifier . Interessierte Leser werden aufgefordert, mehr über diese Konzepte zu lesen. Eine Möglichkeit, den Ausdruck abzuleiten, ist zu finden Hier .
Wir werden den Ausdruck direkt für unseren speziellen Fall bereitstellen, in dem Y. nimmt zwei Klassen {+1, -1} . Wir werden die im vorherigen Abschnitt gezeigte Intuition auch auf den allgemeinen Fall ausweiten, in dem X. kann mehrdimensional sein. Nehmen wir an, es gibt zu unabhängige Variablen. In diesem Fall bedeutet die Klasse & # 120583 -ein und & # 120583 +1 wären Vektoren von Dimensionen k * 1 und die Varianz-Kovarianz-Matrix & # 120622 wäre eine Matrix von Dimensionen k * k .
Die Klassifikatorfunktion ist gegeben als
Y = h (X) = Vorzeichen (b T. X + c)
Wo,
b = -2 & # 120622 -ein (& # 120583 -ein - & # 120583 +1 )
c = & # 120583 -ein T. & # 120622 -ein & # 120583 -ein - & # 120583 -ein T. & # 120622 -ein & # 120583 -ein {-2 ln (1-p) / p}
Die Vorzeichenfunktion kehrt zurück +1 wenn der Ausdruck b T. x + c> 0 , sonst kehrt es zurück -ein . Der natürliche Log-Term in c vorhanden ist, um die Tatsache auszugleichen, dass die Klassenwahrscheinlichkeiten nicht für beide Klassen gleich sein müssen, d.h. p kann ein beliebiger Wert zwischen (0, 1) und nicht nur 0,5 sein.
Modellparameter lernen
Gegeben ein Datensatz mit N. Datenpunkte (x ein , Y. ein ), (x 2 , Y. 2 ),… (X. n , Y. n ) müssen wir schätzen p, & # 120583 -ein , & # 120583 +1 und & # 120622 . Eine statistische Schätztechnik namens Maximum-Likelihood-Schätzung wird verwendet, um diese Parameter zu schätzen. Die Ausdrücke für die obigen Parameter sind unten angegeben.
& # 120583 +1 = (1 / N. +1 ) * & # 120506 i: yi = + 1 x ich
& # 120583 -ein = (1 / N. -ein ) * & # 120506 i: yi = -1 x ich
p = N. +1 / N.
& # 120622 = (1 / N) * & # 120506ich = 1: N. (x ich - & # 120583 ich ) (x ich - & # 120583 ich ) T.
Wo N. +1 = Anzahl der Proben, wobei y ich = +1 und N. -ein = Anzahl der Proben, wobei y ich = -1 .
Mit den obigen Ausdrücken ist das LDA-Modell vollständig. Man kann die Modellparameter unter Verwendung der obigen Ausdrücke schätzen und sie in der Klassifikatorfunktion verwenden, um die Klassenbezeichnung eines neuen Eingabewerts einer unabhängigen Variablen zu erhalten X. .
Fahren wir mit dem Artikel zur linearen Diskriminanzanalyse fort und sehen wir uns das an
Beispiel in R.
Der folgende Code generiert einen Dummy-Datensatz mit zwei unabhängigen Variablen X1 und X2 und eine abhängige Variable Y. . Zum X1 und X2 Wir werden eine Stichprobe aus zwei multivariaten Gaußschen Verteilungen mit Mitteln erzeugen & # 120583 -ein = (2, 2) und & # 120583 +1 = (6, 6) . 40% der Stichproben gehören zur Klasse +1 und 60% gehören zur Klasse -ein , deshalb p = 0,4 .
Bibliothek (ggplot2) Bibliothek (MASS) Bibliothek (mvtnorm) #Varianz Kovarianzmatrix für zufällige bivariate Gauß-Stichprobe var_covar = Matrix (Daten = c (1,5, 0,3, 0,3, 1,5), nrow = 2) # Zufällige bivariate Gauß-Stichproben für Klasse + 1 Xplus1<- rmvnorm(400, mean = c(6, 6), sigma = var_covar) # Random bivariate gaussian samples for class -1 Xminus1 <- rmvnorm(600, mean = c(2, 2), sigma = var_covar) #Samples for the dependent variable Y_samples <- c(rep(1, 400), rep(-1, 600)) #Combining the independent and dependent variables into a dataframe dataset <- as.data.frame(cbind(rbind(Xplus1, Xminus1), Y_samples)) colnames(dataset) <- c('X1', 'X2', 'Y') dataset$Y <- as.character(dataset$Y) #Plot the above samples and color by class labels ggplot(data = dataset)+ geom_point(aes(X1, X2, color = Y)) In der obigen Abbildung repräsentieren die blauen Punkte Stichproben aus der Klasse +1 und die roten repräsentieren die Stichprobe aus der Klasse -ein . Es gibt eine gewisse Überlappung zwischen den Abtastwerten, d. H. Die Klassen können nicht vollständig durch eine einfache Linie getrennt werden. Mit anderen Worten, sie sind nicht perfekt linear trennbar .
Wir werden nun ein LDA-Modell unter Verwendung der obigen Daten trainieren.
# Trainieren Sie das LDA-Modell mit dem obigen Datensatz lda_model<- lda(Y ~ X1 + X2, data = dataset) #Print the LDA model lda_model
Ausgabe:
Frühere Wahrscheinlichkeiten von Gruppen:
-elf
0,6 0,4
Gruppe bedeutet:
public string tostring ()
X1 X2
-1 1,928108 2,010226
1 5.961004 6.015438
Koeffizienten linearer Diskriminanten:
LD1
X1 0,5646116
X2 0,5004175
Wie man sehen kann, sind die vom Modell gelernten Klassenmittel (1.928108, 2.010226) für die Klasse -ein und (5.961004, 6.015438) für die Klasse +1 . Diese Mittelwerte liegen sehr nahe an den Klassenmitteln, mit denen wir diese Zufallsstichproben generiert haben. Die vorherige Wahrscheinlichkeit für die Gruppe +1 ist die Schätzung für den Parameter p . Das b Vektor sind die linearen Diskriminanzkoeffizienten.
Wir werden nun das obige Modell verwenden, um die Klassenbezeichnungen für dieselben Daten vorherzusagen.
#Vorhersagen der Klasse für jede Stichprobe im obigen Datensatz mithilfe des LDA-Modells y_pred<- predict(lda_model, newdata = dataset)$class #Adding the predictions as another column in the dataframe dataset$Y_lda_prediction <- as.character(y_pred) #Plot the above samples and color by actual and predicted class labels dataset$Y_actual_pred <- paste(dataset$Y, dataset$Y_lda_prediction, sep=',') ggplot(data = dataset)+ geom_point(aes(X1, X2, color = Y_actual_pred))
In der obigen Abbildung stammen die lila Proben aus der Klasse +1 die vom LDA-Modell korrekt klassifiziert wurden. Ebenso sind die roten Proben aus der Klasse -ein das wurden richtig klassifiziert. Die blauen sind aus der Klasse +1 wurden aber falsch klassifiziert als -ein . Die grünen sind aus der Klasse -ein die als falsch klassifiziert wurden +1 . Die Fehlklassifizierungen treten auf, weil diese Stichproben näher am anderen Klassenmittelwert (Mitte) liegen als der tatsächliche Klassenmittelwert.
Dies bringt uns zum Ende dieses Artikels von Edureka, einem vertrauenswürdigen Online-Lernunternehmen mit einem Netzwerk von mehr als 250.000 zufriedenen Lernenden auf der ganzen Welt. Mit dem Data Analytics with R-Training von Edureka können Sie Fachkenntnisse in den Bereichen R-Programmierung, Datenmanipulation, explorative Datenanalyse, Datenvisualisierung, Data Mining, Regression, Stimmungsanalyse und Verwendung von R Studio für reale Fallstudien zu Einzelhandel und sozialen Medien erwerben.
Hast du eine Frage an uns? Bitte erwähnen Sie es im Kommentarbereich dieses Artikels und wir werden uns so schnell wie möglich bei Ihnen melden.