Graph Traversal-Methoden haben mich schon immer fasziniert. Von der Durchführung einer effektiven Peer-to-Peer-Kommunikation bis zur Suche nach den nächstgelegenen Restaurants und Cafés mithilfe von GPS haben Traversal-Methoden im realen Szenario eine Vielzahl von Anwendungen. In diesem Blog über den Algorithmus für die Breitensuche werden wir die Logik hinter den Methoden zum Durchlaufen von Graphen diskutieren und anhand von Beispielen die Funktionsweise des Algorithmus für die Breitensuche verstehen.
Um detaillierte Kenntnisse über künstliche Intelligenz und maschinelles Lernen zu erhalten, können Sie sich live anmelden von Edureka mit 24/7 Support und lebenslangem Zugriff.
Hier ist eine Liste der Themen, die sein werden in diesem Blog behandelt:
Beispielcode für logistische Regressionspythons
- Einführung in Graph Traversal
- Was ist die Breitensuche?
- Grundlegendes zum Algorithmus für die Breitensuche anhand eines Beispiels
- Pseudocode des Breitensuchalgorithmus
- Anwendungen der Breitensuche
Einführung in Graph Traversal
Das Aufrufen und Erkunden eines Diagramms zur Verarbeitung wird als Diagrammdurchquerung bezeichnet. Genauer gesagt geht es darum, jeden Scheitelpunkt und jede Kante in einem Diagramm so zu besuchen und zu erkunden, dass alle Scheitelpunkte genau einmal untersucht werden.
Das klingt einfach! Aber da ist ein Fang.
Es gibt verschiedene Techniken zum Durchlaufen von Graphen, z. B. die Breitensuche, die Tiefensuche usw. Die Herausforderung besteht darin, ein Diagramm zu verwenden Traversal-Technik, die am besten zur Lösung eines bestimmten Problems geeignet ist. Dies bringt uns zur Technik der Breitensuche.
Was ist der Breitensuchalgorithmus?
Der Breitensuchalgorithmus ist eine Graph-Traversing-Technik, bei der Sie einen zufälligen Anfangsknoten (Quell- oder Wurzelknoten) auswählen und den Graph schichtweise so durchlaufen, dass alle Knoten und ihre jeweiligen untergeordneten Knoten besucht und untersucht werden.
Bevor wir weiter gehen und die Breitensuche anhand eines Beispiels verstehen, sollten wir uns mit zwei wichtigen Begriffen im Zusammenhang mit der Diagrammdurchquerung vertraut machen:
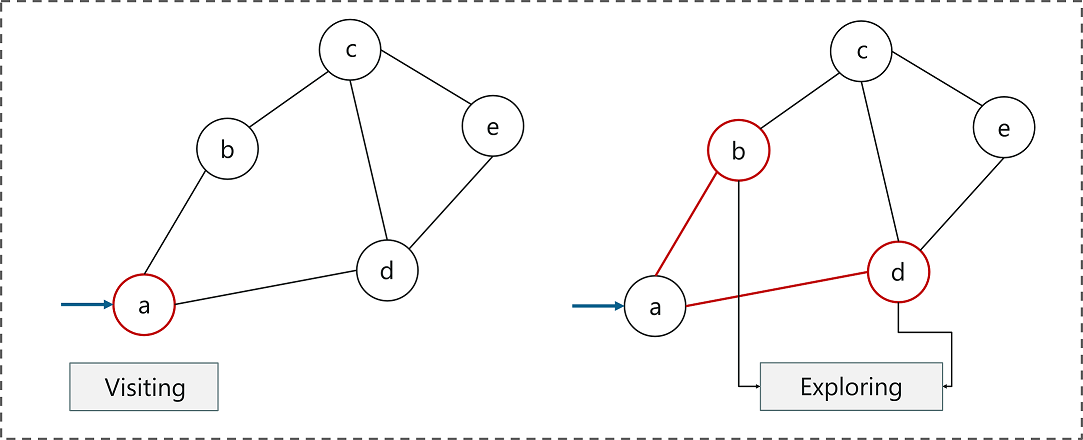
- Besuch eines Knotens: Wie der Name schon sagt, bedeutet der Besuch eines Knotens, einen Knoten zu besuchen oder auszuwählen.
- Einen Knoten erkunden: Erkundung der benachbarte Knoten (untergeordnete Knoten) eines ausgewählten Knotens.
Beziehen Sie sich auf die obige Abbildung, um dies besser zu verstehen.
Grundlegendes zum Breitensuchalgorithmus anhand eines Beispiels
Der Algorithmus für die Breitensuche folgt einem einfachen, stufenbasierten Ansatz zur Lösung eines Problems. Betrachten Sie den folgenden Binärbaum (der ein Diagramm ist). Unser Ziel ist es, den Graphen mithilfe des Breitensuchalgorithmus zu durchlaufen.
Bevor wir beginnen, müssen Sie mit der Hauptdatenstruktur des Algorithmus für die Breitensuche vertraut sein.
Eine Warteschlange ist eine abstrakte Datenstruktur, die der First-In-First-Out-Methode folgt (auf zuerst eingefügte Daten wird zuerst zugegriffen). Es ist an beiden Enden offen, wobei immer ein Ende zum Einfügen von Daten (Enqueue) und das andere zum Entfernen von Daten (Dequeue) verwendet wird.
Schauen wir uns nun die Schritte zum Durchlaufen eines Diagramms mithilfe der Breitensuche an:
Schritt 1: Nehmen Sie eine leere Warteschlange.
Schritt 2: Wählen Sie einen Startknoten (Besuch eines Knotens) und fügen Sie ihn in die Warteschlange ein.
Schritt 3: Sofern die Warteschlange nicht leer ist, extrahieren Sie den Knoten aus der Warteschlange und fügen Sie seine untergeordneten Knoten (Erkunden eines Knotens) in die Warteschlange ein.
Schritt 4: Drucken Sie den extrahierten Knoten.
Machen Sie sich keine Sorgen, wenn Sie verwirrt sind. Wir werden dies anhand eines Beispiels verstehen.
Schauen Sie sich das folgende Diagramm an. Wir verwenden den Algorithmus für die Breitensuche, um das Diagramm zu durchlaufen.
In unserem Fall weisen wir den Knoten 'a' als Wurzelknoten zu und beginnen mit dem Durchlaufen nach unten und befolgen die oben genannten Schritte.
Das obige Bild zeigt den End-to-End-Prozess des Breitensuchalgorithmus. Lassen Sie mich dies näher erläutern.
- Weisen Sie 'a' als Stammknoten zu und fügen Sie es in die Warteschlange ein.
- Extrahieren Sie den Knoten 'a' aus der Warteschlange und fügen Sie die untergeordneten Knoten von 'a' ein, d. H. 'B' und 'c'.
- Druckknoten 'a'.
- Die Warteschlange ist nicht leer und hat die Knoten 'b' und 'c'. Da 'b' der erste Knoten in der Warteschlange ist, extrahieren wir ihn und fügen die untergeordneten Knoten von 'b' ein, d. H. Die Knoten 'd' und 'e'.
- Wiederholen Sie diese Schritte, bis die Warteschlange leer ist. Beachten Sie, dass die bereits besuchten Knoten nicht zur Warteschlange hinzugefügt werden sollten nochmal.
Schauen wir uns nun den Pseudocode des Breadth-First Search-Algorithmus an.
Pseudocode des Breitensuchalgorithmus
Hier ist der Pseudocode zum Implementieren des Breitensuchalgorithmus:
Eingabe: s als Quellknoten BFS (G, s) lassen Q Warteschlange sein. Q.enqueue (s) markiert s als besucht, während (Q ist nicht leer) v = Q.dequeue () für alle Nachbarn w von v in Grafik G, wenn w nicht besucht wird. Q.enqueue (w) markiert w als besucht
Im obigen Code werden die folgenden Schritte ausgeführt:
- (G, s) wird eingegeben, hier ist G der Graph und s ist der Wurzelknoten
- Eine Warteschlange 'Q' wird erstellt und mit dem Quellknoten 's' initialisiert.
- Alle untergeordneten Knoten von 's' sind markiert
- Extrahieren Sie 's' aus der Warteschlange und besuchen Sie die untergeordneten Knoten
- Verarbeiten Sie alle untergeordneten Knoten von v
- Speichert w (untergeordnete Knoten) in Q, um die untergeordneten Knoten weiter zu besuchen
- Fahren Sie fort, bis 'Q' ist leer
Bevor wir den Blog abschließen, schauen wir uns einige Anwendungen des Breadth-First Search-Algorithmus an.
Anwendungen des Breitensuchalgorithmus
Die Breitensuche ist eine einfache Methode zum Durchlaufen von Graphen mit einem überraschenden Anwendungsbereich. Hier sind einige interessante Möglichkeiten, wie Bread-First Search verwendet wird:
Crawler in Suchmaschinen: Die Breitensuche ist einer der Hauptalgorithmen für die Indizierung von Webseiten. Der Algorithmus beginnt mit dem Durchlaufen der Quellseite und folgt allen mit der Seite verknüpften Links. Hier wird jede Webseite als Knoten in einem Diagramm betrachtet.
GPS-Navigationssysteme: Die Breitensuche ist einer der besten Algorithmen, um mithilfe des GPS-Systems benachbarte Standorte zu finden.
Finden Sie den kürzesten Pfad und den minimalen Spannbaum für ein ungewichtetes Diagramm: Wenn es um ein ungewichtetes Diagramm geht, ist die Berechnung des kürzesten Pfades recht einfach, da die Idee hinter dem kürzesten Pfad darin besteht, einen Pfad mit der geringsten Anzahl von Kanten auszuwählen. Die Breitensuche kann dies ermöglichen, indem eine Mindestanzahl von Knoten ausgehend vom Quellknoten durchlaufen wird. In ähnlicher Weise können wir für einen Spanning Tree eine der beiden Methoden Breadth-First Search oder Depth-First Traversal verwenden, um einen Spanning Tree zu finden.
Rundfunk: Das Netzwerk nutzt das, was wir als Pakete für die Kommunikation bezeichnen. Diese Pakete folgen einer Durchquerungsmethode, um verschiedene Netzwerkknoten zu erreichen. Eine der am häufigsten verwendeten Traversal-Methoden ist die Breitensuche. Es wird als Algorithmus verwendet, mit dem gesendete Pakete über alle Knoten in einem Netzwerk übertragen werden.
Peer-to-Peer-Netzwerk: Die Breitensuche kann als Durchquerungsmethode verwendet werden, um alle benachbarten Knoten in einem Peer-to-Peer-Netzwerk zu finden. Beispielsweise verwendet BitTorrent die Breitensuche für die Peer-to-Peer-Kommunikation.
Das war also alles über die Funktionsweise des Breadth-First Search-Algorithmus. Jetzt, da Sie wissen, wie man Diagramme durchläuft, sind Sie sicher neugierig, mehr zu erfahren. Hier sind einige relevante Blogs, die Sie interessieren:
Damit kommen wir zum Ende dieses Blogs. Wenn Sie Fragen zu diesem Thema haben, hinterlassen Sie bitte unten einen Kommentar. Wir werden uns dann bei Ihnen melden.
Wenn Sie sich für einen vollständigen Kurs über künstliche Intelligenz und maschinelles Lernen anmelden möchten, hat Edureka einen speziell kuratierten Kurs Dadurch beherrschen Sie Techniken wie überwachtes Lernen, unbeaufsichtigtes Lernen und Verarbeitung natürlicher Sprachen. Es umfasst Schulungen zu den neuesten Fortschritten und technischen Ansätzen im Bereich künstliche Intelligenz und maschinelles Lernen wie Deep Learning, grafische Modelle und Reinforcement Learning.