Mit einfachen Worten, Rekursion ist eine Möglichkeit, das Problem zu lösen, indem ein Funktionsaufruf selbst ausgeführt wird: Das Wort „ rekursiv 'Stammt aus dem lateinischen Verb' wiederkehren ”, Was bedeutet, etwas zu wiederholen. Dies ist, was die rekursive Funktion tut, sie wiederholt immer wieder dasselbe, d. H. Sie erinnert sich. In diesem Artikel lernen wir die Rekursion in Python kennen. Im Folgenden sind die Themen aufgeführt, die in diesem Blog behandelt werden:
- Was ist Rekursion in Python?
- Kündigungsbedingung
- Pythons Rekursionslimit
- Abflachen von Listen mit Rekursion
- Vorteile der Rekursion
- Nachteile der Rekursion
Was ist Rekursion in Python?
Rekursion ist der Prozess, etwas in Bezug auf sich selbst zu bestimmen. Wir wissen, dass in Python jede Funktion jede andere Funktion aufrufen kann, eine Funktion kann sich auch selbst aufrufen. Diese Arten von Funktionen, die sich selbst aufrufen, bis die bestimmte Bedingung nicht erfüllt ist, werden als rekursive Funktionen bezeichnet.
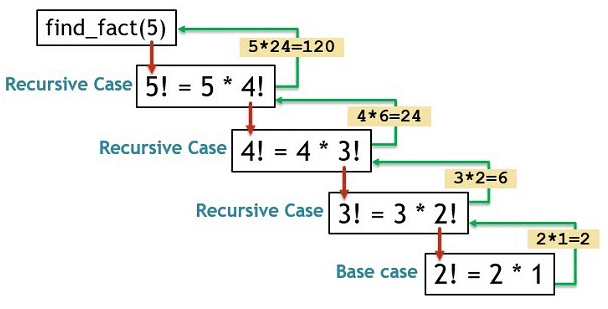
Nehmen wir ein paar Beispiele, um zu sehen, wie das funktioniert. Wenn Sie eine positive ganze Zahl n erhalten, wäre die Fakultät.
- n! = n * (n-1) * (n-2) und so weiter.
- 2! = 2 * (2-1)
- ein! = 1
- 0! = 0
- 4! = 4 * 3!
- 3! = 3 * 2!
- 2! = 2 * 1!
Das Ersetzen der obigen Werte führt zu folgendem Ausdruck
- 4! = 4 * 3 * 2 * 1
Wir müssen eine Funktion definieren, sagen wir Fakt (n), die eine positive ganze Zahl oder 0 als Parameter verwendet und die n-te Fakultät zurückgibt. Wie können wir das mit Rekursion tun?
Mal sehen, um dies mit Rekursion zu tun, müssen wir die folgende Gleichung untersuchen
n! = n. (n-1). (n-2) & hellip3.2.1
n! = n. (n-1)! #Wir können die obige Anweisung wie in dieser Zeile umschreiben
Wenn wir nun 2 als Parameter übergeben, erhalten wir:
2! = 2.1! = 2
In ähnlicher Weise erhalten wir, wenn wir 1 bestehen:
Java findet die größte Nummer in der Liste
ein! = 1,0! = 1
Aber wenn wir 0 übergeben, bricht es
0! = 0. (- 1)! und hier ist Fakultät für -1 nicht definiert, so dass dies nur für Werte> 0 funktioniert
Wir müssen also zwei Fälle schreiben
1. n! = n. (n-1)! wenn n> = 1
2. 1 wenn n = 0
Dies ist eine vollständige Lösung für alle positiven ganzen Zahlen und 0.
Wie benutzt man Logger in Java?
Kündigungsbedingung
Eine rekursive Funktion muss eine wichtige Bedingung erfüllen, um beendet zu werden. Wenn Sie sich einem Zustand nähern, in dem das Problem ohne weitere Rekursion gelöst werden kann, wird eine rekursive Funktion beendet, wodurch das Problem in kleinere Teilschritte minimiert wird. Eine Rekursion kann in einer Endlosschleife enden, wenn die Beendigungsbedingung in den Aufrufen nicht erfüllt ist.
Faktorielle Bedingungen:
- Fakultät von n = n * (n-1), solange n größer als 1 ist.
- 1 wenn n = 0
Wir werden die obigen faktoriellen Bedingungen in Python-Code konvertieren:
def fact (n): wenn n == 1: return n else: return n * fact (n-1)
Nehmen wir ein Beispiel, wir wollen eine Fakultät von 4 finden:
fact (4) #dies gibt 4 * fact (3) usw. zurück, bis n == 1 ist.
Ausgabe: 24
Es wird aufgrund seiner Einfachheit und Klarheit so oft als Beispiel für eine Rekursion verwendet. Lösen kleinerer Problemfälle bei jedem Schritt, der als Rekursion in der Informatik bezeichnet wird.
Pythons Rekursionslimit
In einigen Sprachen können Sie eine Endlosschleife erstellen, in Python gibt es jedoch eine Rekursionsbeschränkung. Um das Limit zu überprüfen, führen Sie die folgende Funktion vom sys-Modul aus. Dies gibt die Grenze der für Python festgelegten Rekursion an.
import sys sys.getrecursionlimit ()
Ausgabe: 1000
Sie können das Limit auch mithilfe der Funktionen setrecursionlimit () des sys-Moduls entsprechend Ihren Anforderungen ändern. Erstellen Sie nun eine Funktion, die sich selbst rekursiv aufruft, bis sie das Limit überschreitet, und überprüfen Sie, was passiert:
def recursive (): recursive () wenn __name__ == '__main__': recursive ()
Wenn Sie den obigen Code ausführen, wird eine Laufzeitausnahme angezeigt: RuntimeError: Die maximale Rekursionstiefe wurde überschritten. Python verhindert, dass Sie eine Funktion erstellen, die in einer nie endenden rekursiven Schleife endet.
Abflachen von Listen mit Rekursion
Andere Dinge, die Sie mithilfe der Rekursion tun können, mit Ausnahme von Fakultäten. Angenommen, Sie möchten eine Single aus einer verschachtelten Liste erstellen. Dies können Sie mit dem folgenden Code tun:
def flatten (a_list, flat_list = none): Wenn flat_list none ist: flat_list = [] für Element in a_list: if isinstance (Element, Liste): flatten (Element, flat_list) else: flat_list.append (Element) return flat_list if __name__ == '__main__': verschachtelt = [1,2,3, [4,5], 6] x = flacher (verschachtelter) Druck (x)
Ausgabe: [1,2,3,4,5,6]
Das Ausführen des obigen Codes führt zu einer einzelnen Liste anstelle einer Ganzzahlliste mit einer Ganzzahlliste, die wir als Eingabe verwendet haben. Sie können dasselbe auch auf andere Weise tun. Python hat so etwas wie itertools.chain (). Sie können den Code überprüfen, der zum Erstellen einer Funktionskette verwendet wird (). Es ist ein anderer Ansatz, dasselbe zu tun wie wir.
Vorteile der Rekursion
Der Code ist sauber und elegant in einer rekursiven Funktion.
Eine zusammengesetzte Aufgabe kann mithilfe der Rekursion in einfachere Unterprobleme unterteilt werden.
Das Generieren von Sequenzen ist mit Rekursion einfacher als mit verschachtelten Iterationen.
wie man Power in Java macht
Nachteile der Rekursion
Es kann manchmal schwierig sein, der Logik hinter der rekursiven Funktion zu folgen.
Rekursive Anrufe sind teuer (ineffizient), da sie viel Speicher und Zeit in Anspruch nehmen.
Rekursive Funktionen sind schwer zu debuggen.
In diesem Artikel haben wir gesehen, was Rekursion ist und wie wir aus der Problemstellung rekursive Funktionen entwickeln können, wie mathematisch eine Problemstellung definiert werden kann. Wir haben ein Problem der Fakultät gelöst und die Bedingungen ermittelt, die erforderlich sind, um Fakultäten zu finden, aus denen wir diese Bedingungen in Python-Code konvertieren konnten, um Ihnen das Verständnis der Funktionsweise der Rekursion zu vermitteln. Ich finde es gut, dass Python eine integrierte Grenze für die Rekursion hat, um zu verhindern, dass Entwickler schlecht konstruierte rekursive Funktionen erstellen. Eine wichtige Sache, die zu beachten ist, ist, dass die Rekursion schwer zu debuggen ist, da sich die Funktion immer wieder selbst aufruft.